TIPO DE FUNCIONES

     Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio son también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
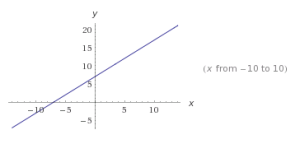
Una función lineal de una única variable independiente x suele escribirse en la forma siguiente y= mx+b
que se conoce como ecuación de la recta en el plano xy.
m es denominada la pendiente de la recta.
b es la ordenada en el origen, el valor de y para x= 0, es el punto (0,b). 
     

      Funciones cuadráticas resulta de interés no sólo en matemática sino también en física y en otras áreas del conocimiento como por ejemplo: la trayectoria de una pelota lanzada al aire, la trayectoria que describe un río al caer desde lo alto de una montaña, la forma que toma una cuerda floja sobre la cual se desplaza un equilibrista, el recorrido desde el origen, con respecto al tiempo transcurrido, cuando una partícula es lanzada con una velocidad inicial.

         Función cuadrática responde a la formula: y= a x2 + b x + c con a =/ 0. Su gráfica es             una curva            llamada parábola cuyas características son:
        Si a es mayor a 0 es cóncava y admite un mínimo. Si a es menor a 0 es convexa y                 admite un máximo.
         Vértice: Puntos de la curva donde la función alcanza el máximo o el mínimo.
          Eje de simetría: x = xv.
          intersección con el eje y.
         Intersecciones con el eje x: se obtiene resolviendo la ecuación de segundo grado

      Las funciones trigonométricas son valores sin unidades que dependen de la                     magnitud       de un ángulo. Se dice que un ángulo situado en un plano de coordenadas      rectangulares      está en su posición normal si su vértice coincide con el origen y su lado       inicial coincide con la parte positiva del eje x.